Написать программу или программы для получения решения уравнения теплопроводности
![]()
аналитическим методом, явным центрально-разностным методом и соответствующим варианту неявным методом. Начальные условия выбрать в соответствии с предлагаемым вариантом задания. Граничные условия нулевые. Решение ищем в пространственной области ![]() .
.
Предусмотреть возможность вычисления до заданного момента времени или до сходимости. Предусмотреть возможность вывода данных как для заданного момента времени, так и для всего расчётного отрезка времени с заданным шагом.
Провести следующие расчёты:
- сквозной расчёт до сходимости (обозначим время
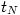 ); отобразить результаты на графике;
); отобразить результаты на графике; - расчёт до момента времени
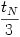 с выводом полученных в данный момент времени результатов; отобразить результаты на графике;
с выводом полученных в данный момент времени результатов; отобразить результаты на графике; - расчёт до сходимости с выводом результатов в моменты времени
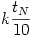 ; отобразить результаты на графике в виде поверхности.
; отобразить результаты на графике в виде поверхности.
| Вариант | Метод решения | Начальные условия |
|---|---|---|
| 1 | неявная центрально-разностная схема | 1 |
| 2 | схема Кранка — Николсона | 2 |
| 3 | неявная центрально-разностная схема | 3 |
| 4 | схема Кранка — Николсона | 1 |
| 5 | неявная центрально-разностная схема | 2 |
| 6 | схема Кранка — Николсона | 3 |
Приложение 1
Точное аналитическое решение
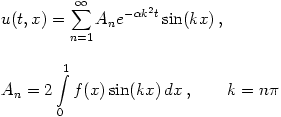
для начальных и граничных условий вида
![]()
Приложение 2
Явная центрально-разностная схема
![]()
Неявная центрально-разностная схема
![]()
Схема Кранка — Николсона
![]()
Приложение 3
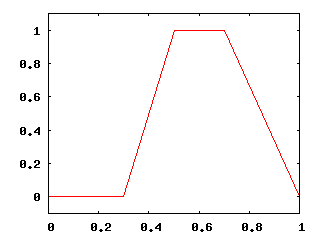
Начальное распределение 1
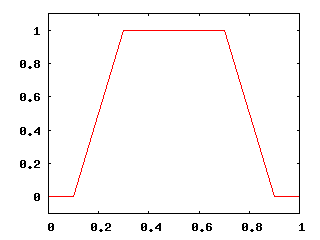
Начальное распределение 2
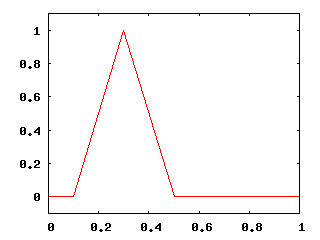
Начальное распределение 3