Написать программу или программы для получения решения одномерного уравнения переноса
- аналитическим методом;
- неявным центрально-разностным (эйлеровым) методом;
- соответствующим варианту явным методом.
Начальные условия выбрать в соответствии с предлагаемым вариантом задания. Граничные условия нулевые (
). Решение ищем в пространственной области 
.
Предусмотреть возможность вычисления до заданного момента времени, к выбору которого следует подойти аккуратно; необходимо обеспечить одинаковое значение времени полученного решения для всех используемых методов. Сравнить полученные результаты, представив их на одном графике. Объяснить различия.
Варианты заданий
| Вариант | Метод решения | Начальные условия |
|---|---|---|
| 1 | Явный метод Эйлера | 1 |
| 2 | Метод Лакса — Вендроффа | 2 |
| 3 | Метод Мак-Кормака | 3 |
| 4 | Явный метод Эйлера | 2 |
| 5 | Метод Лакса — Вендроффа | 3 |
| 6 | Метод Мак-Кормака | 1 |
| 7 | Явный метод Эйлера | 3 |
| 8 | Метод Лакса — Вендроффа | 1 |
| 9 | Метод Мак-Кормака | 2 |
По результатам лабораторной работы следует подготовить отчёт, содержащий необходимые графики и развёрнутое описание полученных результатов, собственную оценку данных результатов и сделать далеко идущие выводы. К отчёту желательно приложить программный код.
Отчёт в формате PDF высылается на адрес const@mail.ru. Заголовок письма должен содержать фамилию автора, номер группы и номер лабораторной работы.
Приложение 1
Точное аналитическое решение
для начальных условий вида
Приложение 2
Неявный центрально-разностный метод Эйлера
Приложение 3
Явный метод Эйлера с разностями против потока
Метод Лакса — Вендроффа
Метод Мак-Кормака
Предиктор:
Корректор:
Приложение 4
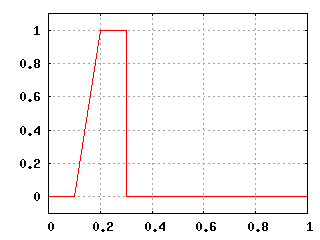
Начальное распределение 1
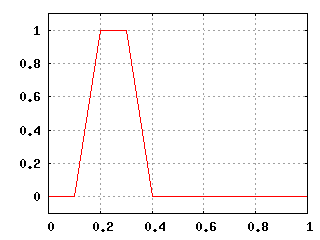
Начальное распределение 2
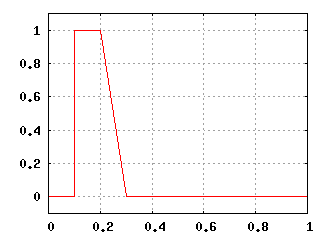
Начальное распределение 3
