Лабораторная работа содержит два задания.
Особенность данной работы проявляется в требовании к используемому языку программирования: он должен обладать явной статической типизацией. То есть языки типа С/С++ или Fortran подходят для выполнения данной лабораторной работы, тогда как Python или Matlab — нет
Задание 1
Вычислить значение экспоненты при помощи ряда Тейлора:
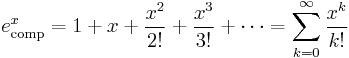
В качестве условия сходимости ряда следует взять отношение
Сравниить полученный результат с точным значением
Следует произвести вычисления для 
.
Объясните полученный результат.
Комментарий. При выполнении первого задания следует воспользоваться максимально прямолинейным алгоритмом вычисления суммы ряда. Именно такой подход позволит наиболее полно выявить исследуемый вид погрешности.
Задание 2
Вычислить производную экспоненты при помощи конечно-разностного выражения первого порядка точности:
Сравнить полученный результат с точным значением (получить погрешность) 
.
Вычисления следует произвести при 
для разных значений 
, где 
.
Выполнить задание дважды: с использованием вещественных переменных и переменных двойной точности; результаты представить на графике 
с использованием логарифмической шкалы.
Объяснить полученный результат.
По результатам лабораторной работы следует подготовить отчёт, содержащий необходимые графики и развёрнутое описание полученных результатов, собственную оценку данных результатов и далеко идущие вывод с точки зрения использования вычислительного моделирования. К отчёту желательно приложить программный код.
Отчёт в формате PDF высылается на адрес const@mail.ru. Заголовок письма должен содержать фамилию автора, номер группы и номер лабораторной работы.